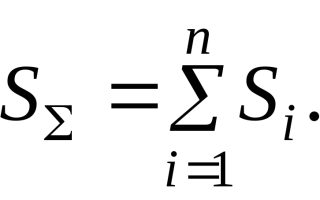Погрешность и неопределённость
Стандартизация, направленная на достижение оптимальной степени упорядочения в определенной области посредством установления соответствующих норм, требований и правил, и сертификация, подтверждающая соответствие качества продукции, процессов или услуг этим требованиям, нормам и правилам, в современных условиях являются основными способами повышения конкурентоспособности предприятия,Классификация. Погрешность измерений,Классификация неопределенностей измерений,Формируемые метрологические характеристики средств измерений — выбор СИ,Методические погрешности измерений примеры,Суммирование погрешностей